关于成人高考专升本·高等数学二中《条件概率与事件的独立性》的考点，包括：条件概率的概念及相关公式、事件的独立性和条件概率与事件的独立性等知识点，具体内容如下：

　　考点一：条件概率的概念及相关公式

　　(1)条件概率的概念

　　设A、B为同一随机试验的两个事件，且P(B)>0，则称P(A|B) 为在事件B发生的条件下，事件A发生的条件概率.且

　　P(A|B)=P(AB)/P(B)

　　(2)条件概率的相关公式

　　①乘法公式

　　对任意两事件A，B，若P(A)>0，则P(AB)=P(A)P(B|A).

　　一般地，设A₁，A₂，…，An，为任意n个事件，若P(A₁A₂……An-₁)>0，则P(A₁A₂…An) =P(A₁) P(A₂|A₁)·P(A₃|A₁A₂)·…·P(An|A₁A₂…An-₁)

　　②全概率公式

　　设随机试验对应的样本空间为Ω，设A₁，A₂，…，An是样本空间Ω的一个划分，B是任意一个事件，则

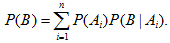
　　注：设事件A₁，A₂，…，An满足如下两个条件：

　　(i)A₁，A₂，…，An，互不相容，且P(Ai)>0，i=1，2，…，n；

　　(ii)A₁∪A₂∪…∪An=Ω， 即A₁，A₂，…，An，至少有一个发生，则称A₁，A₂，…，An，为样本空间Ω的一个划分.

　　当A₁，A₂，…，An，是Ω的一个划分时，每次试验有且只有其中的一个事件发生.

　　③贝叶斯公式

　　设A₁，A₂，…，An是样本空间的一个划分，B是任一事件，且P(B)>0，则

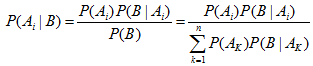
　　i=1，2，…，n.

　　考点二：事件的独立性

　　(1)如果P(AB)=P(A)·P(B)，则称事件A，B是相互独立的.

　　(2)设A₁，A₂，…，An为n个事件，如果对于任意整数k(1≤k≤n)和任意k个整数1≤i₁<i₂<…<iĸ≤n，有

　　P(Ai₁Ai₂…Aiĸ)=P(Ai₁)P(Ai₂).....P(Aiĸ)，

　　则称事件A₁，A₂，…，An，相互独立，简称A₁，A₂，…An，独立；如果对于任意两个整数1≤i₁≤i₂≤n，有P(Ai₁Ai₂)=P(Ai₁)·P(Ai₂)，则称事件A₁，A₂，…,An两两独立.

　　考点三：条件概率与事件的独立性

　　(1) 一般地，P(AB) =P(A)·P(B|A) =P(B)·P(A|B) .

　　(2)随机事件A₁，A₂，…，An相互独立一定两两独立；反之，它们两两独立不一定相互独立.

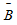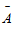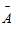　　(3)如果A与B事件相互独立，则A与，与B，与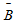也都相互独立.

　　(4)事件A与B相互独立的充要条件

　　①若P(A)>0，则A与B相互独立的充要条件是P(B) =P(B|A).

　　②若P(B)>0，则A与B相互独立的充要条件是P(A) =P(A|B).