考点1  随机变量

　　设E是随机试验，样本空间为Ω，如果对于每一个结果(样本点)ω∈Ω，有一个实数X(ω)与之对应，这样就得到一个定义在Ω上的实值函数X=X(ω)，则称其为随机变量.随机变量通常用X，Y，Z，…(或X1，X2，…)来表示.

　　考点2  离散型随机变量

　　若随机变量X只取有限多个或可列无限多个值，则称X为离散型随机变量.

　　考点3  离散型随机变量的概率分布

　　设离散型随机变量X的一切可能值为x1，x2，…，xk，…，且对应于x1，x2，…，xk，…有P{X=xk}=pk(k=1，2，…，n)，则称上式为离散型随机变量的概率分布或分布律(列)，常以表格的形式列出.

　　考点4  随机变量的分布函数

　　设X为一随机变量，称函数F(x)=P{X≤x}(-∞<x<∞)为X的分布函数.

　　考点5  0-1分布、二项分布和泊松分布的分布律

　　注：此部分内容，考生可根据自己的情况进行掌握

　　(1)0-1分布

　　若随机变量X只取两个可能值：0,1，且

　　P{(X=1}=p，P{X=0}=q，

　　其中0<p<1，q=1-p，则称X服从0-1分布.X的分布律为

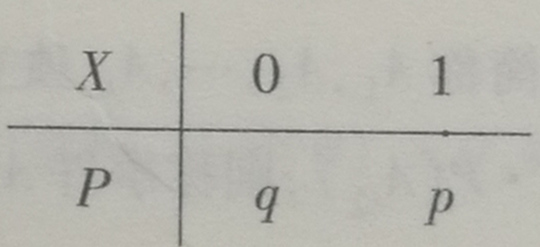
　　(2)二项分布

　　若随机变量X的可能取值为0,1，…,n，而X的分布律为

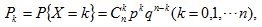
　　其中0<p<1，p+q=1，则称X服从参数为n，p的二项分布，简记为X~B(n,p).

　　显然，当n=1时，X服从0-1分布，即0-1分布实际上是二项分布的特例.

　　(3)泊松分布

　　设随机变量X的可能取值为0,1,…,n,…,而X的分布律为

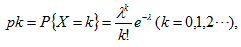
　　其中λ>0，则称X服从参数为λ的泊松分布，简记为X~P(λ).

　　考点6  随机变量的基本理论

　　1.概率分布的性质有：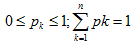 

　　2.分布函数有如下性质：

　　(1)0≤F(x)≤1.

　　(2)F(x)是不减函数.

　　(3)

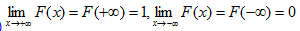
　　(4)P(x≤b)=F(b).

　　(5)P(a<X≤b)=P(X≤b)-P(X≤a)=F(b)-F(a)(a<b).特别地

　　P(X>a)=1-P(X≤a)=1-F(a).