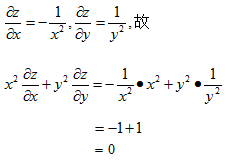2019年成人高等学校招生全国统一考试专升本

高等数学(二)

　　本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间150分钟.

　　第Ⅰ卷(选择题，共40分)

　　一、选择题(1~10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的)

　　1. 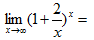【D】

　　A.-e²  B.-e  C.e  D.e²

　　【考情点拨】本题考查了两个重要极限的知识点.

　　【应试指导】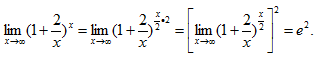

　　2.设函数y=arcsinx，则y'=【B】

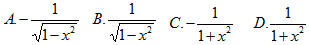
　　【考情点拨】本题考查了函数的导数公式的知识点.

　　【应试指导】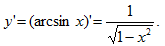

　　3.设函数f(x)在[a,b]上连续，在(a,b)可导，f()>0，f(a)f(b)<0，则f(x)在(a,b)零点的个数为【C】

　　A.3  B.2  C.1  D.0

　　【考情点拨】本题考查了零点存在定理的知识点.

　　【应试指导】由零点存在定理可知，f(x)在(a,b)上必有零点，且函数是单调函数，故其在(a,b)上只有一个零点.

　　4.设函数y=x³+eˣ，则y⁴=【B】

　　A.0 B.eˣ C.2+eˣ D.6+eˣ

　　【考情点拨】本题考查了高阶导数的知识点.

　　【应试指导】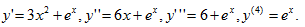

　　5. 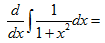【C】

　　A.arctanx  B.arccotx  C.1/(1+x²)  D.0

　　【考情点拨】本题考查了不定积分的性质的知识点.

　　【应试指导】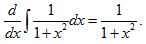

　　6.∫cos2xdx=【A】

　　A.(1/2)sin2x+C B.-(1/2)sin2x+C C.(1/2)cos2z+C D.-(1/2)cos2x+C

　　【考情点拨】本题考查了不定积分公式的知识点.

　　【应试指导】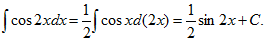

　　7. 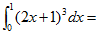【D】

　　A.-10  B.-8  C.8  D.10

　　【考情点拨】本题考查了定积分的计算的知识点.

　　【应试指导】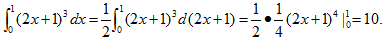

　　8.设函数x=(x-y)¹⁰，则 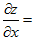【C】

　　A.(x一y)¹⁰  B.-(x-y)¹⁰  C.10(x-y)⁹  D.-10(x-y)⁹

　　【考情点拨】本题考查了偏导数的知识点.

　　【应试指导】由偏导数公式可得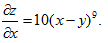

　　9.设函数x=2(x-y)-x²-y²，则其极值点为【D】

　　A.(0,0) B.(-1,1) C.(1,1) D.(1,-1)

　　【考情点拨】本题考查了二元函数极值的知识点.

　　【应试指导】易知 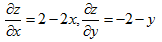，令 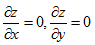 ，得驻点(1,-1)，

　　而 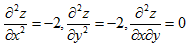 故△=0-(-2)·(-2)=-4<0，因此(1,-1)是函数的极值点.

　　10.设离散型随机变量X的概率分布为

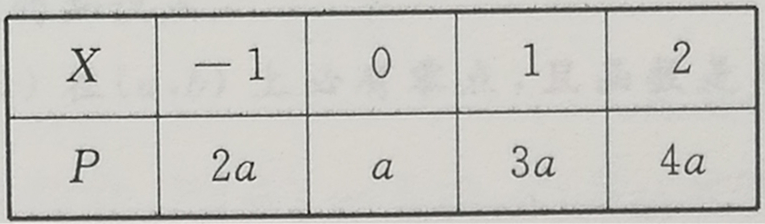
　　则a=【A】

　　A.0.1  B.0.2  C.0.3  D.0.4

　　【考情点拨】本题考查了概率的性质的知识点.

　　【应试指导】由概率分布的性质可知2a+a+3a+4a=10a=1，a=0.1.

　　第Ⅱ卷(非选择题，共110分

　　二、填空题(11~20小题，每小题4分，共40分)

　　11.当x→0时f(x)与3x是等价无穷小，则 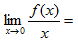_3_.

　　【考情点拨】本题考查了等价无穷小的知识点.

　　【应试指导】由题可知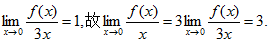 

　　12.

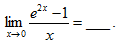
　　【答案】2

　　【考情点拨】本题考查了极限的知识点.

　　【应试指导】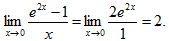

　　13.设函数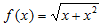，则f'(1)=___.

　　【答案】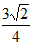

　　【考情点拨】本题考查了导函数的知识点.

　　【应试指导】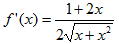，因此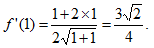

　　14.设x²为f(x)的一个原函数，则f(x)=_2x_.

　　【考情点拨】本题考查了不定积分的原函数的知识点.

　　【应试指导】由题意可知∫f(x)dx=x²+C，故f(x)=(∫f(x)dx)'=(x²+C)'=2x.

　　15.设函数y=lnsinx，则dy=_cotxdx_.

　　【考情点拨】本题考查了微分的知识点.

　　【应试指导】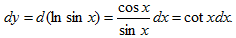

　　16.

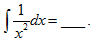
　　【答案】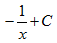

　　【考情点拨】本题考查了不定积的计算的知识点.

　　【应试指导】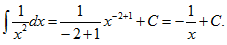

　　17.

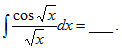
　　【答案】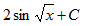

　　【考情点拨】本题考查了复合函数的不定积分的知识点.

　　【应试指导】

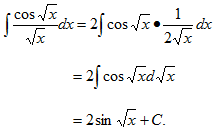
　　18. 

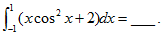
　　【答案】4

　　【考情点拨】本题考查了定积分的计算的知识点.

　　【应试指导】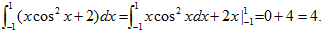

　　19.设函数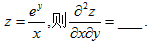

　　【答案】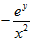 

　　【考情点拨】本题考查了二阶偏导数的知识点.

　　【应试指导】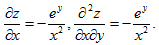

　　20.设函数x=sinx·lny，则dz=___.

　　【答案】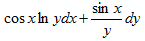

　　【考情点拨】本题考查了二元函数的全微分的知识点.

　　【应试指导】

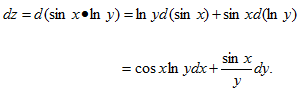
　　三、解答题(21~28题，共70分.解答应写出推理、演算步骤)

　　21.(本题满分8分)

　　计算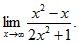 

　　【答案】 

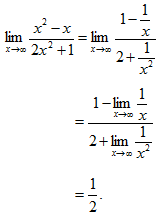
　　22.(本题满分8分)

　　设函数 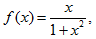 求f'(x).

　　【答案】 

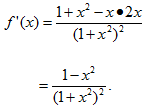
　　23.(本题满分8分)

　　计算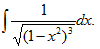 

　　【答案】 令x=sint，-(π/2)<t<(-π/2)，则有dx=costdt,

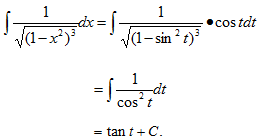
　　而t=arcsinx，故有

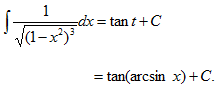
　　24.(本题满分8分)

　　计算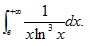 

　　【答案】 

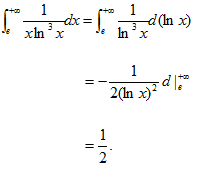
　　25.一个袋中有10个乒乓球，其中7个橙色，3个白色，从中任取2个，设事件A为“所取的2个乒乓

　　球颜色不同”，求事件A发生的概率P(A).(本题满分8分)

　　【答案】 A为所取的2个乒乓球颜色不同，即A表示所取的2个球中1个球是橙色，一个球是白色，

　　故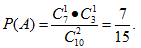 

　　26.(本题满分10分)

　　设函数f(x)=ax³+bx²+cx在x=2处取得极值，点(1,-1)为曲线y=f(x)的拐点，求a,b,c.

　　【答案】易知f'(x)=3ax²+2bx+c，f''(c)=6ax+2b，由于f(x)在x=2处取得极值，则f'(2)=12a+4b+c=0，点(1,-1)是y=f(x)的拐点，故有f(1)=-1，f''(1)=0，即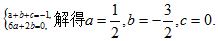

　　27.已知函数f(x)的导函数连续，且 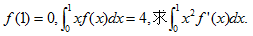(本题满分10分)

　　【答案】

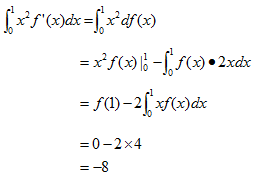
　　28.设函数 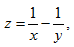 证明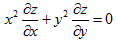：  (本题满分10分)

　　【答案】