关于成人高考专升本·高等数学一中定积分的几何意义、函数可积条件和定积分的性质等知识考点，具体内容如下：

　　考点1 定积分的几何意义

　　若在区间[a,b]上f(x)>0，则定积分 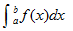的值为由曲线y=f(x)，直线x=a，x=b，y=0所围成图形即曲边梯形的面积，即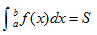 

　　若在[a,b]上f(x)<0，则积分值为负，这个负数的相反数即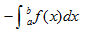表示由曲线y=f(x)，直线x=a，x=b，y=0所围图形的面积，即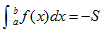 

　　若f(x)在[a,b]内有正有负，则 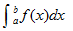表示曲线y=f(x)，直线x=a，x=b及x轴所成的各部分图形的面积代数和，即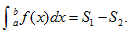 

　　考点2 函数可积条件

　　1.y=f(x)在[a,b]上可积的必要条件是f(x)在[a,b]上有界.

　　2.y=f(x)在[a,b]上可积的充分条件是f(x)在[a,b]上连续.

　　考点3 定积分的性质

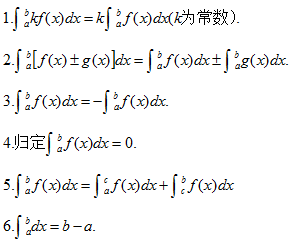
　　7.若在区间[a,b]上有f(x)≤g(x)，则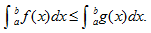 

　　8.设m，M为函数f(x)在区间[a,b]上的最小值，最大值，则

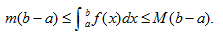
　　9.在区间[a,b]上恒有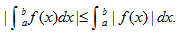 

　　[注]在性质7、8、9中都有前提条件，在区间[a,b]上，即下限小，上限大，否则全不成立.

　　10.定积分中值定理

　　若函数f(x)在闭区间[a,b]上连续，则至少存在一点：ξ∈[a,b]，使 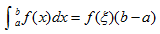成立，则称f(ξ)或称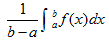为函数f(x)在区间[a,b]上的平均值.